Expected Goals and Uncertainty
Introduction
My Twitter feed seems to be increasingly taken up with discussions of Expected Goals in football, yet there always seems to be something important missing from the discussion, and that's uncertainty.
What Are Expected Goals
Due to the way most expected goals models have been developed, when we refer to expected goals we are typically talking about the probability of an average player scoring a goal from an average shot taken from a certain situation on the pitch - for example taking a header at location x, y, from a chance originating from a through ball.
While this provides a reasonable estimate as to what happens over the long term for that type of shot, it fails to accurately represent the individual shot we are attempting to measure.
Pierre-Simon Laplace suggested back 1814 in his Philosophical Essay on Probabilities that if you know the precise location and momentum of every atom in the universe, their past and future values can be calculated. But in the real world we don't have that level of detail, just a bunch of data scraped off the internet. We have no idea of the ball's momentum, whether it's spinning, what the position of the defenders are, how well the goalkeeper is positioned, whether the attacking player is off balance, the direction of the wind, whether the attacking player is nursing an injury, how good the attacking player is at shooting, and so on.
As well as the uncertainty due to this lack of information, there is also the uncertainty of the model itself. We are not training the model on every shot that's ever been taken, rather we are using a subset of shots and that in itself adds to our uncertainty. This is known as the sampling error, and is the difference between the true value for a statistic and the value we've estimated from our sample of data.
No two shots taken from the same situation are ever exactly the same, and even if they were we cannot be certain enough of the estimate from our model to assign a single, absolute value to the output.
Uncertainty
This doesn't necessarily mean that expected goals are useless, but that more care needs to be taken of their usage. Instead of a single value, expected goals need to convey their uncertainty using techniques such as confidence intervals.
Confidence intervals provide an estimated range likely to contain the true value at a set confidence level. So instead of just saying a shot is worth 0.25 expected goals, we would say say the shot was worth 0.25 ± 0.1 expected goals at the 95% confidence level. This essentially means that we are 95% confident the true value of expected goals for that particular shot lies somewhere in the range of 0.15 - 0.35.
Sure, it's not so snappy but it conveys so much more information then the single value does. There is huge variability in expected goals through lack of information, sample sizes and the general randomness of football. By just using the central estimate you are missing out on a lot of information, and potentially sharing misleading numbers too.
For example, take a look at Figure One below showing the cumulative expected goals by minute from a match between Norwich City and Sunderland.
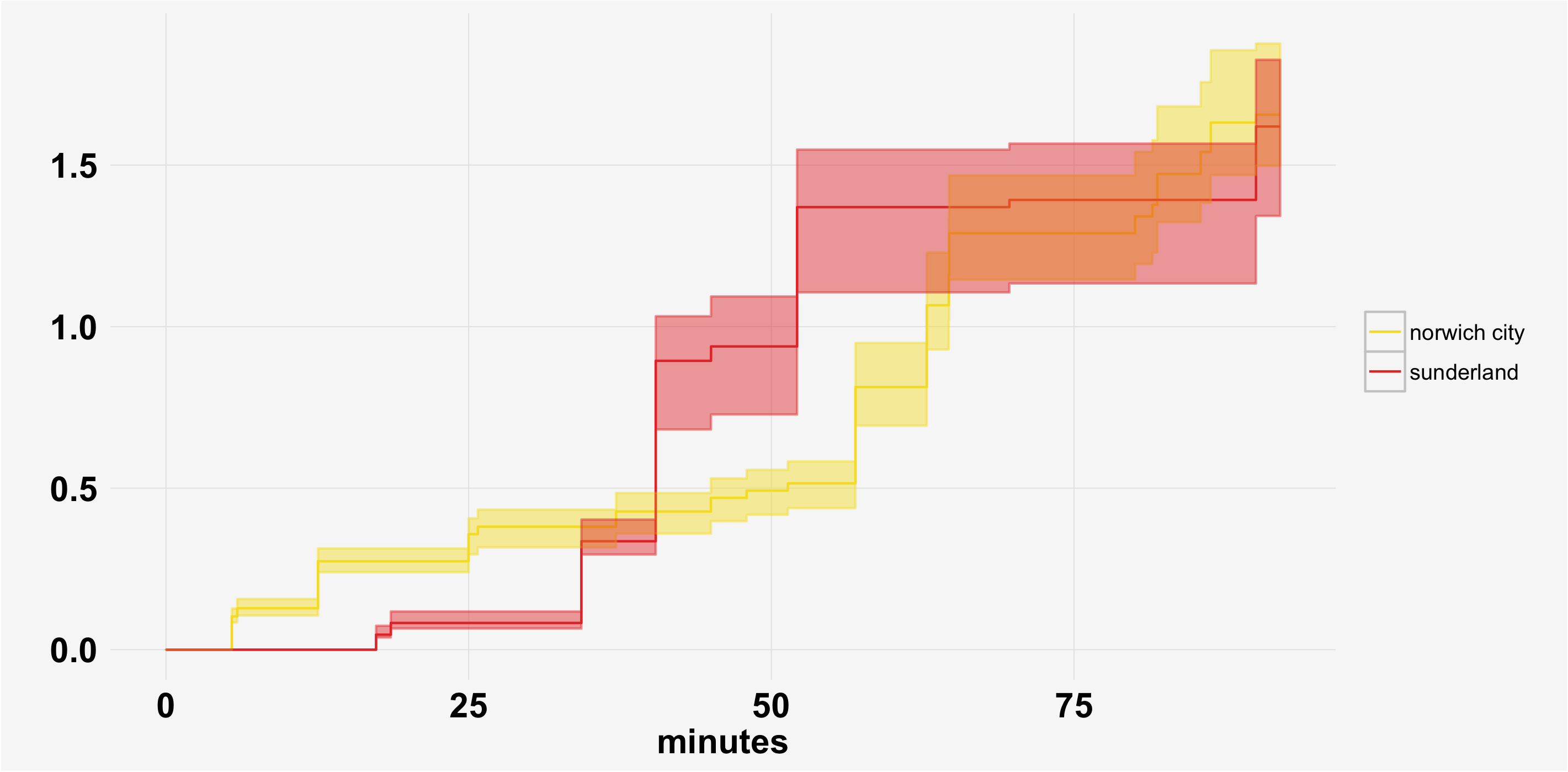Figure One: Cumulative Expected Goals By Minute
The lines show the central estimate for the total expected goals surrounded by the 95% confidence intervals. Around minute 68 Sunderland's central estimate is higher than Norwich's suggesting they have been the better team in terms of expected goals. If you look closer though, due to the high variance associated with Sunderland's shots the bottom of their confidence interval actually stretches below the bottom of Norwich's, suggesting its's feasible for Sunderland to actually have a lower expected goals total than Norwich at that point of the game.
Even when you move towards larger sample sizes and look at expected goals by team over the course of a season (Figure Two), you still see huge variability that you'll potentially be mislead by when you ignore the uncertainty. Plus, there's some really interesting information in there, like how Crystal Palace's goals against total has a narrower range than West Bromwich Albion's. Who'd have though that??
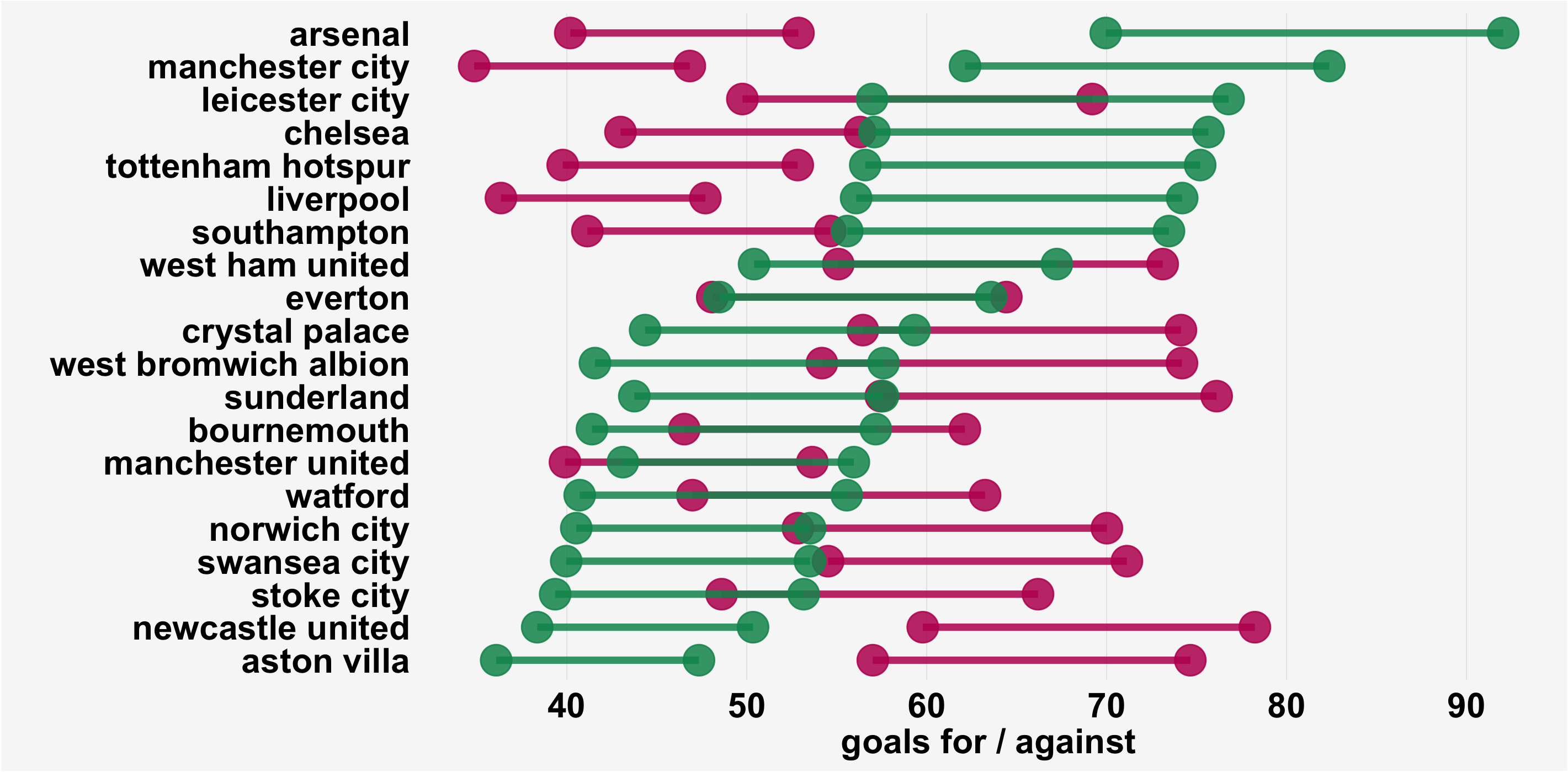Figure Two: Expected Goals By Team For 2014/2015
Conclusions
The variance associated with expected goals, especially at the level of individual matches (let alone individual shots!!), is such that the uncertainty needs to be clearly accounted for. Without this information, expected goals are at best an inaccurate measure and at worst misleading or wrong.
Embrace the uncertainty and include confidence intervals!