Expected Goals Updated
Introduction
When I introduced my Expected Goals model a few weeks back a number of people commented on the bump in the curve where I had included penalty shots in the data set used to fit the model. The reason I’d originally left penalties in was I felt their number was too few to have an impact on the fit of the model and at the time I hadn’t actually tracked which shots were and were not from penalties.
Since that decision seemed to cause quite a kerfuffle I have since gone back to the raw data, removed all the penalties and refitted the curve. While I was at it I also added in more shots I had collected and rescaled all the co-ordinates to use a larger pitch (105 x 68m) as Claus Moeller had suggested my estimate of Premier League pitch size was too small.
As expected, the difference in the fit of the curve is very small (Figure 1) but it has pushed the r squared value up to 0.86 from 0.84, meaning that 86% of the variance in goal scoring is due to the distance from the goal the shot is taken from and just 14% is due to other reasons, such as player talent, defensive pressure, goalkeeper etc.
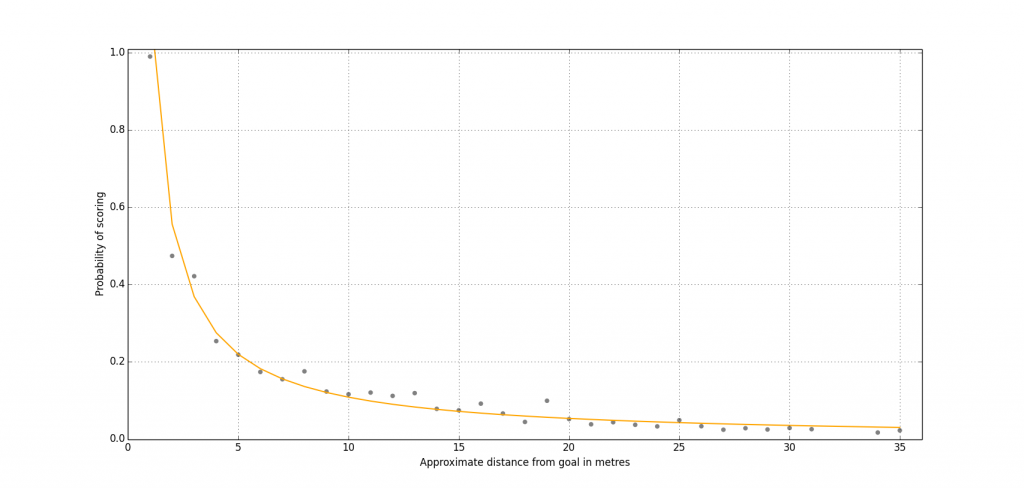Figure 1: Shots Versus Distance From Goal
The equation for expected goals is now updated to -1.014718 for the coefficient and 0.05082859 for the intercept so for my previous example a shot from 8 metres gives:
$8^{-1.014718}*10^{0.05082859}=0.1362846$ expected goals