PlayerRating: A Bayesian Method For Evaluating Football Players
Introduction
I originally submitted the idea behind this article to the recent Opta Pro Forum and although it was turned down I thought I’d write it up anyway incase anyone else was interested in the results.
Plus/Minus
The premise of my abstract was that while the plus/minus score is popular in the analysis of many sports, such as NHL and MLB, it hasn't taken off in football. And there is a good reason for that - it’s hard to do.
For anyone who hasn’t come across them before, plus/minus scores measure a team's goal difference while an individual player is on the pitch. Players with a positive score are considered to have a favourable effect on the team’s overall performance while those with a negative score are causing the team to perform worse.
It’s a simple concept that sounds feasible enough but it has a big flaw in that it treats all players equally so is biased towards players on good teams. Think what would happen if you put me into Barcelona’s first team, they’d probably still win more matches than they’d lose and I’d have a positive plus/minus making me look like a great footballer. In reality, I’d have been flailing around hopelessly and would have been lucky to have even touch the ball let alone made a positive contribution.
The Adjusted Plus/Minus
One solution to this bias is the adjusted plus/minus. This incorporates a linear regression in to the calculation to account for the effect of all the other players on the pitch during the match in order to avoid a player’s score being inflated by his team mates.
However, as Howard Hamilton has previously shown on his blog, the adjusted plus/minus doesn’t work well for football. With only three substitutes per team and 38 league matches per season there is little data available to cover all the possible combinations of players. Plus some players, such as goalkeepers in particular, play a large portion of the available minutes making it virtually impossible to distinguish the true effect of removing them from the team. And with football being such a low scoring game there is a lot of noise in the data increasing the regression’s prediction errors.
As an example, here’s the current top 10 best players as rated by adjusted plus/minus scores for the English Premier league so far this season.
| Player |
| Joleon Lescott |
| Ahmed El Mohamadi |
| Tom Heaton |
| Jonas Olsson |
| Ashley Williams |
| Gareth Barry |
| Wes Morgan |
| Victor Moses |
| Oussama Assaidi |
| Steven NZonzi |
Now, I don’t know about you but I’m pretty sure Joleon Lescott is not the league’s best player. And what about some of the Premier League’s big stars? Well, Cesc Fàbregas is rated as the 86th best player, Diego Costa is 199th and Sergio Agüero is down in position 256. In fact the error for Sergio Agüero’s plus/minus score is so high that we can’t even tell whether he has a positive or negative rating. Yep, according to the adjusted plus/minus Sergio Agüero may actually be having a negative effect on Manchester City’s performances this season. Okaaay then.
Regularised Adjusted Plus/Minus
The next step from here is to try and reduce the errors by moving from a standard linear regression to a ridge regression. I’m not going to go into too much detail as again Howard Hamilton has a great article on this but the idea is that ridge regression helps minimise the errors associated with the player’s plus/minus scores. As with everything in life though, there is no such thing as a free lunch and by making the regression behave better we incorporate some bias into the results. But is it worth it? Nope, the results using ridge regression still have too much error to be useful. Hands up if you think Chris Smalling is the Premier League’s best player. Nobody? Right, let's move on then.
Next Steps
So now what? One of the major problems we have is a lack of data for many of the players so let's take a more Bayesian approach and add in something called a Prior. These are basically probability distributions covering some aspect of what we want to predict that expresses our uncertainty before we account for the evidence. Where we don’t have much data this Prior helps inform our predictions but as we accumulate more data the Prior’s influence decreases and the real evidence holds more weight.
Okay, that probably sounds a bit complicated if you don’t have a maths background so here’s an example: imagine you’re watching a footballer play for the first time, there is a chance the player may be as good as Lionel Messi, there is a chance they may be as bad as Tom Cleverley, and there is a chance they may be somewhere in-between and be average. As the game progresses you see them play and form your conclusion as to whether they're any good or not.
This is essentially how my PlayerRating model works. Based on preliminary data it constructs a set of Priors and estimates the probability of the player being world class, average or stealing a living in the sport. As the player’s career progresses the model gains more data about them and the estimates iteratively move away from the Prior towards the Player’s true rating.
PlayerRating
The PlayerRating model works by combining a number of factors for each player into a single rating. This rating is typically very small so to try and keep things a bit more understandable they get rescaled to centre them around 100 and make them look a little bit like a percentage. It’s not really a percentage but since everyone is familiar with that kind of number it's hopefully a bit less scary.
So what do the results look like? Well, as a starting point here is the current top twenty rated players:
| Player | Rating |
| Lionel Messi | 174 |
| Cristiano Ronaldo | 173 |
| Sergio Ramos | 163 |
| Cesc Fàbregas | 162 |
| Thomas Müller | 160 |
| Philipp Lahm | 158 |
| Bastian Schweinsteiger | 157 |
| Rafinha | 157 |
| Manuel Neuer | 156 |
| Wayne Rooney | 155 |
| Mesut Özil | 155 |
| Piqué | 155 |
| Karim Benzema | 153 |
| Iker Casillas | 151 |
| Iniesta | 150 |
| Javier Mascherano | 148 |
| Toni Kroos | 148 |
| Jérôme Boateng | 147 |
| Ángel Di María | 145 |
And just for the fun of it here are Lionel Messi and Cristiano Ronaldo’s careers to date:
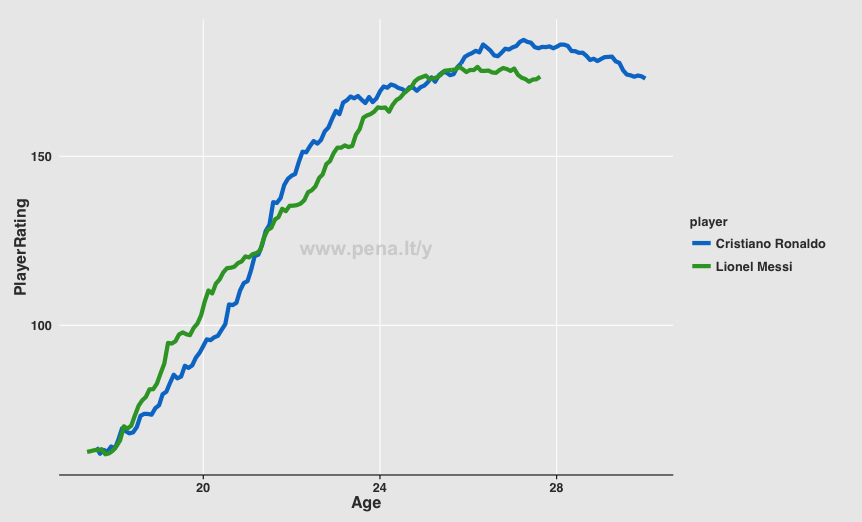
What Next?
This is still really early stages and the work is far from finished but I wanted to get something up on the blog as it will encourage me to keep working on it and to document its progress. The next step is to dig through the data further to gain a better understanding of where this approach is working / not working so well and start to refine things. For example, goalkeepers are currently treated the same as outfield players and I suspect their ratings may be improved by having their own set of Priors.
After that there are lots of other things I want to take a look at, such as how well the ratings predict the trajectory of the player’s remaining career, how to extract confidence intervals, what's the effect of swapping an individual player out of a team and so on. My todo list is growing at a rapid rate!
At some point I’m also going to need to optimise things if I decide to continue with this idea as the ratings are pretty intense to compute. Currently, they are updated in monthly intervals and each month takes around twelve hours to process so it’s not exactly quick to tweak parameters and see the effect! There are some obvious steps to speed things up, such as distributing the processing across multiple cores or computers etc that'll provide some easy wins but no doubt the underlying maths can be optimised too. Plus, it’s all in R which doesn’t help so it may be time to dust off my C++ compiler for bits of the code...
Anyway, let me know what you think. Good idea? Bad idea? Waste of time? Do the results look feasible? Ruining football with numbers (again)?!?! (actually, if you think the last one you really don’t need to let me know!!!)
Comments
Frank Dijkstra - March 03, 2015
Where is Robben? Shouldn't he be in the top 20?
Martin Eastwood - March 03, 2015
Hi Frank - he's in position 21, with a rating marginally lower than Ángel Di María
Mustafa - March 03, 2015
Hey Martin, interesting idea. I'd like to see where this will take you...but it's easy for me to say, you're the one doing all that intense computing :D
So, I guess the PlayerRating works like a predictive model where you feed it the parameters and it gives you the scores you mentioned, right? Correct me if I'm wrong (I'm no statistician), the one thing I could think would be an issue is if you have an emerging player who you wouldn't have enough data on...let's say Barca's emerging talent El Haddadi vs the more refined Luis Suarez. How would that effect my decision as a manager when I look at your model to try to figure out which one to sub into the game? Again, good job and interesting idea.
Martin Eastwood - March 03, 2015
Yes, that's a very good point Mustafa. With younger players there is much less data available so we cannot have as much confidence in our predicted scores meaning we are more cautious and our Priors hold more weight. The number of minutes played is a factor within the model so as a player gains more game time he/she will move further towards their true values so it's important to think about age. A 19 year-old with a PlayerRating of 100 is likely to be very good as they will likely develop and improve their rating, while a 30 year-old has probably already peaked and their rating will probably only worsen with time. I will try to discuss this in more detail in a future article to make it clearer.
Jonas - March 04, 2015
Is it fair to assume the computation time is due to MCMC sampling, and not because of the size of your data? And that chart, is it the Maximum A Posteriori estimate? An alternative to MCMC is INLA, which has a R package that, on the surface at least, resembles the good old glm() function. I don't know if INLA is suitable for your approach, but it is worth looking into. One of the people working involved with INLA is Gianluca Baio, who has also done some bayesian modeling of football results. http://www.r-inla.org/home
Martin Eastwood - March 05, 2015
Cool, r-inla looks really interesting, I'd not seen that before. Thanks Jonas!
Trey - March 07, 2015
Very nice! Do you have the code and data posted anywhere?
Martin Eastwood - March 07, 2015
Thanks Trey, it's still very much a work in progress at the moment and looks like spaghetti code so in no state to share!
Mitchell Wesson - March 07, 2015
Martin,
First of all, great idea. One thing I'd be curious to see is how closely your ratings match some like EA Sport's FIFA franchise or Football Manager's.
You mention in the Adjusted Plus/Minus section the difficulty with accounting for inflation due to the other players on the pitch. How does your Bayesian approach account for potential inflation?
Martin Eastwood - March 07, 2015
Cool idea Mitchell, do you know if a list of the EA Sport ratings are available anywhere?
Vasilis - March 10, 2016
Hi Martin, I have a question. Where do you find your data, and in which program/language do you build your models? Do you use an exponential weighted rational in how you take into consideration your Priors? It would be awsome if you could provide in a future article a more practical example of your rating system, not in full details apparently, but maybe a simple naive example to better understand the concept.
Martin Eastwood - March 10, 2016
Hi Vasilis,
The data has been scraped from as many different websites as I can find that provide scores, line ups, fixture stats and player stats etc. It's all written in Python and I have a variety of scripts running that crawl websites looking for new data, parse it, store it in a database and periodically recalculate the players' ratings.