Massey Ratings For Football Part One
Introduction
We all know the league table can lie and one of the common causes of this is strength of schedule. Take Southampton, at the time of writing they are currently second in the Premier League twelve matches in yet still haven’t played Chelsea, Manchester City, Manchester United or Arsenal. Without wishing to be dismissive of Southampton, who undoubtedly are a very talented team, there’s a pretty decent chance that they’d currently be lower down the league table had these fixtures come up earlier in the season instead of Leicester, Hull or Aston Villa.
Massey Ratings
So if we can’t rely on the league table to tell us which teams are performing best what do we do? One alternative is to use Massey Ratings. This is a method devised by Ken Massey back in 1997 for his honours thesis that rates teams based on what opposition they’ve played. The system was originally designed for American Football but it can be adapted to football fairly trivially.
The idea behind Massey Ratings is that they rate teams such that the difference between any two teams is equal to the expected margin of victory between them, as shown in Equation One below:
$y=ra–rb$
where y is the margin of victory for fixture, ra is the rating of team a, rb is the rating of team b
Error
In an ideal world we’d have enough data that we could calculate true ratings for each team but with players moving from one team to another and with football seasons typically lasting just 38 matches we never have sufficient data for that so we have to settle for approximating ratings based on previous match results. This means we need to modify equation one to add in an error term to allow us to account for any unexplained variation in the outcome of games (Equation Two below).
$y=ra–rb+e$
where y is the margin of victory, ra is the rating of team a, rb is the rating of team b and e is the remaining error in the model.
So far so good, but how do we know what ra and rb should equal? Well, to start with we want that error term we added into Equation Two to be as small as possible so we use a technique called Least Squares to find the optimal set of ratings for each team in order to minimise e based on the past data we have.
The Matrix
Things get slightly trickier here but let’s say our past data comprises m matches involving n teams. We know what the margin of victory was for each match and who won but not the ratings for each team so we have m equations we need to solve to find the n unknown rating values, which we can write as Equation 3 below:
$y=Xr+e$
Where y is the the margin of victory, r is the rating we are trying to find, e is the remaining error and X is an m x m sized matrix of coefficients where each row represents a matchup containing a 1 for the winning team and -1 for the losing team. Unfortunately though, this gives us a very sparse matrix that is likely to be highly over-determined making it difficult to find a unique solution to the system.
The Massey Matrix
Thankfully Massey discovered that you can modify the matrix such that the diagonal elements equal the number of games each teams has played and the off-diagonal elements equal the negation of the number of matchups teams have played against each other giving Equation Four below:
$p=Mr$
where M is the modified Massey Matrix, p is a vector of the score differentials and r is the vector of unknown scores.
We are getting closer now but the matrix still doesn’t necessarily have a unique set of Ratings so Massey modifies it further to set the bottom row to zero and the corresponding element of p to zero too. This constraint creates a full rank matrix for us and forces the ratings to sum to zero.
Massey Ratings For The English Premier League
Finally, using some linear algebra we can solve the system and get the ratings for each team, shown below in Figure One.
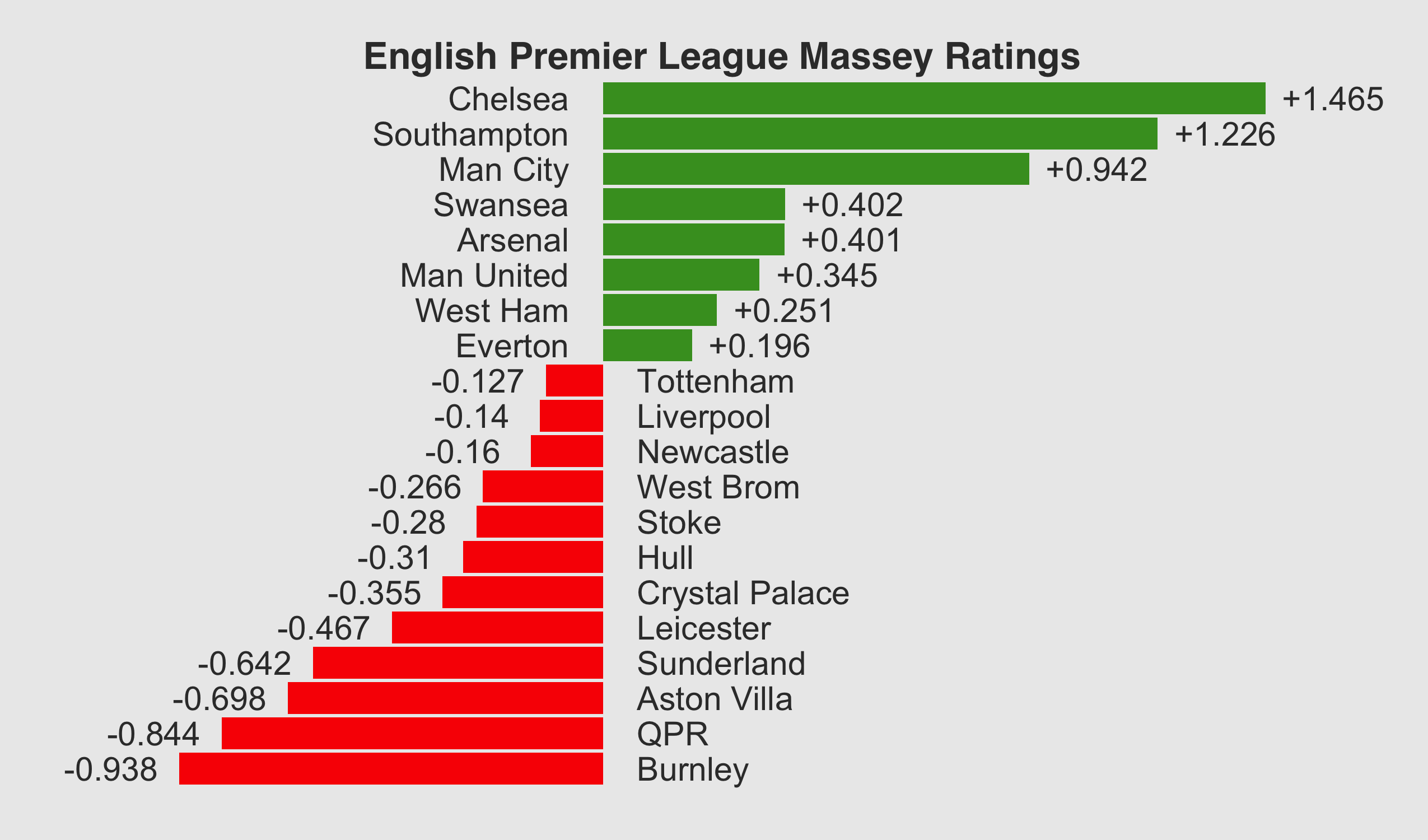Figure One: EPL Massey Ratings
It’s no surprise that Chelsea are ranked far ahead of anybody else in first place but Southampton do actually get ranked in second place, showing that even accounting for their easier schedule to date they deserve to be second in the league at the moment.
Interestingly, Swansea get ranked fourth rather than their current position of seventh in the league. However, Swansea have already played five of the six teams above them so their Massey Rating shows they are performing better than their raw points tally would suggest.
At the bottom of the table it’s not looking good for Aston Villa. I showed in my last article how their Pythagorean meant they were over performing being even as high as they are and this is now backed up by their Massey Rating ranking them in one of the relegation spots.
Next Steps
In my next article I’ll show how we can take Massey Ratings a step further and decompose teams’ overall ratings into separate ratings for both attack and defence. I’ll also add some example code too so you can have a go calculating them yourself.
In the meantime, if you are interested in finding out more about the maths behind Massey Ratings then take a look at Ken Massey’s honours thesis which goes into the theory in much more depth than my brief overview here.
Comments
I OF DICE - February 12, 2017
I think this methodology is attributable to Leake (1976) and Stefani (1977) and not Massey. Check out iofdice.com for an introduction to the methods and their history. Massey (1997) also shows how one can incorporate home field advantage, but that was first introduced by Stefani (1980). Check out my recent post on home field advantage... (https://iofdice.com/2017/02/11/least-squares-ranking-part-vii-home-field-advantage/).
Martin - February 12, 2017
Thanks for the link I OF DICE, I've not seen your site before and will take a look!