Understanding Total Shot Ratio in Football
Introduction
The use of Total Shot Ratio (or TSR) seems to have slowly been gaining ground so I thought it would be worth analyzing the statistic in more detail to see what it can and cannot do.
What is Total Shot Ratio?
Put simply Total Shot Ratio is the proportion of shots taken by one team compared with another. It can be calculated by dividing the number of shots taken by a team by the total shots overall (Figure 1).
$TSR=ShotsFor/(ShotsFor+ShotsAway)$
Figure 1: Total Shot Ratio
It is often used as a surrogate for dominance as the presumption is that the team taking the majority of the shots will be controlling the match and possibly limiting the opposition’s ability to shoot at goal.
Total Shot Ratio Data
Using data taken from the football-data.co.uk website I calculated the Total Shot Ratios for all matches from the English Premier League going back to the 2001-2002 season, giving a total of 8360 data points, which are normally distributed (Figure 2).
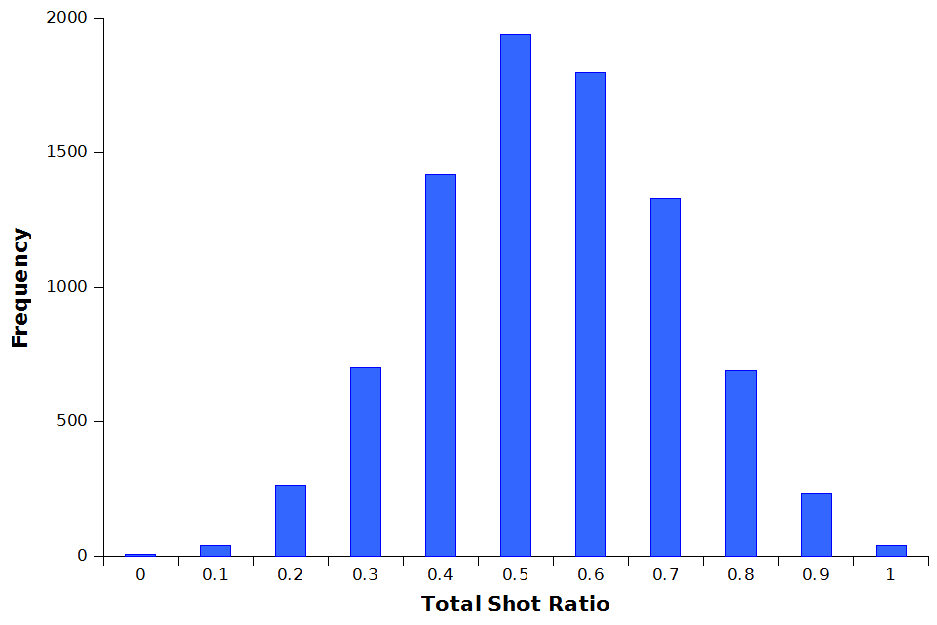Figure 2: Distribution of Total Shot Ratios
The average Total Shot Ratio is always 0.5, because for every value above 0.5 you always an equivalent value below it for the opposition. For example, if the home team’s Total Shot Ratio is 0.75 then the away team’s ratio must be 0.25.
$(0.75 + 0.25) / 2 = 0.5$
The standard deviation, which is a measure of the dispersion of the data around the average value, was 0.166.
Total Shot Ratio: Correlation With Goals Scored
Since Total Shot Ratios are being used to show dominance in a match it makes sense to assess the correlation with the number of goals scored. The higher a team’s Total Shot Ratio is then the more shots it is having compared with the opposition so the expectation would be that they would score more goals. However, this does not seem to be the case as the relationship between the two is extremely weak (Figure 3; r2=0.079).
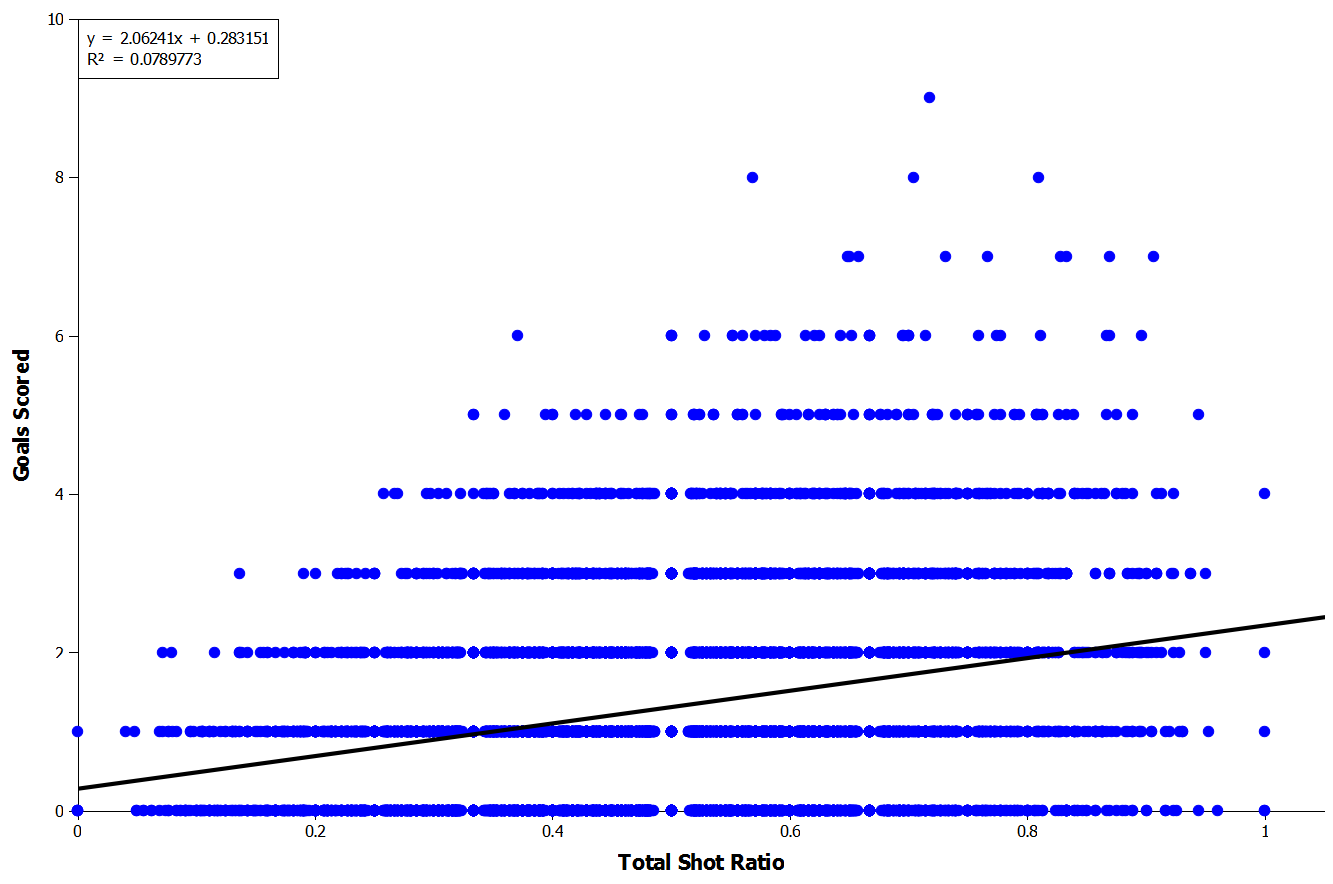Figure 3: Correlation Between Total Shot Ratio and Goals Scored
Total Shot Ratio: Correlation With Goal Difference
So how about the relationship between Total Shot Ratio and goal difference instead? Since teams with higher Total Shot Ratios are thought to be dominating matches, perhaps they are more likely to have a higher goal difference in the match as they may also be less likely to concede goals? Again though the correlation is weak (Figure 4, r2=0.11).
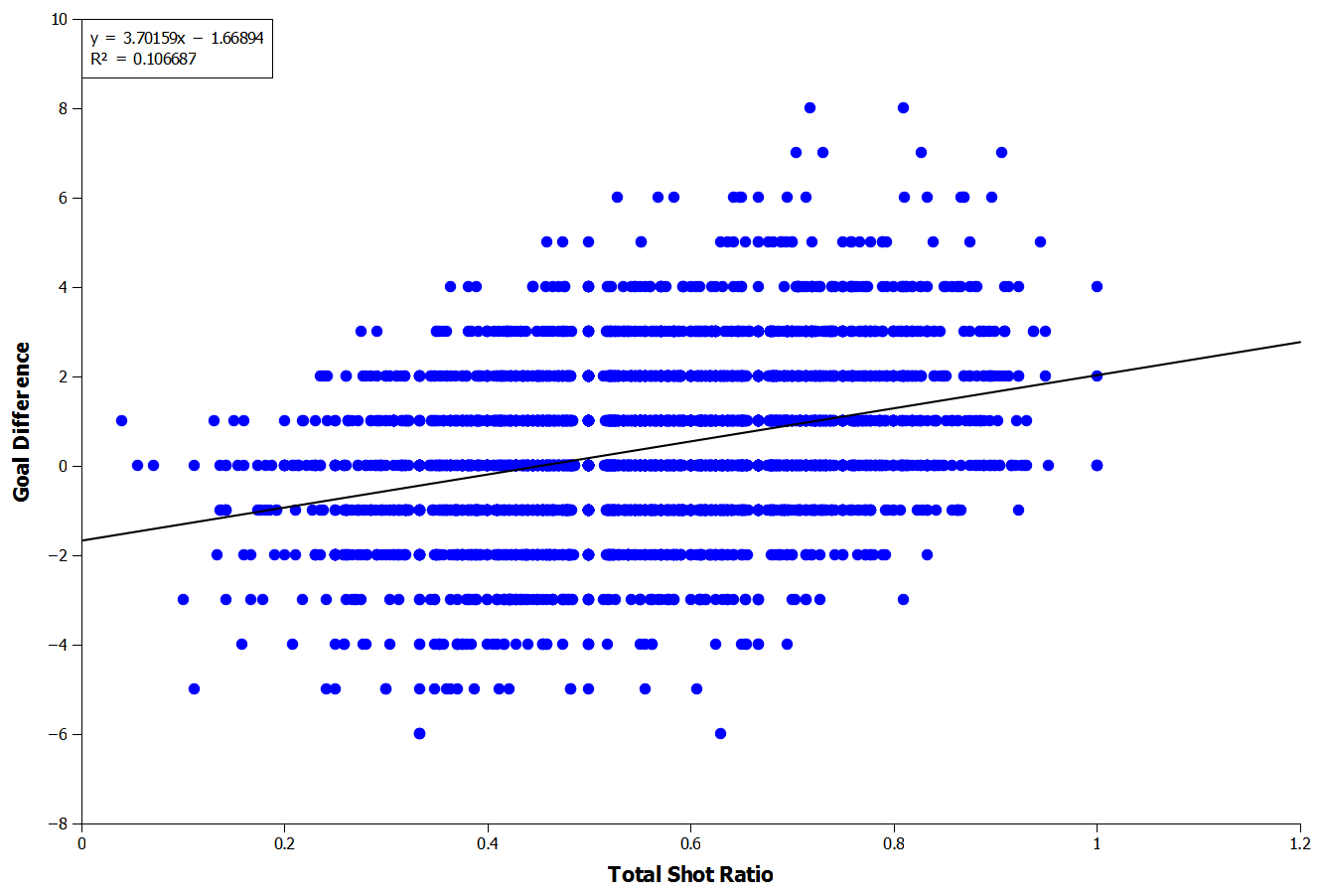Figure 4: Correlation Between Total Shot Ratio and Goal Difference
Total Shot Ratio: Correlation With Match Outcomes
Additionally, the relationship between Total Shot Ratio and match outcome is also poor (r2=0.066) suggesting that Total Shot Ratio also has very little influence on the likelihood of a team winning a particular match. Just because you are taking a greater proportion of the shots does not mean you are any more likely to win.
Total Shot Ratio: Correlation With Points Per Season
Although the match-by-match correlations above are weak there is the suggestion of a trend so it may be that Total Shot Ratio is heavily luck driven in the short term and that we need more matches before we can see the overall effects of a higher ratio. For example, looking at the correlation between Total Shot Ratio and points over an entire season shows a pretty decent relationship between the two (Figure 5). This suggests that long term possessing a higher Total Shot Ratio is in fact associated with fewer matches being lost per season.
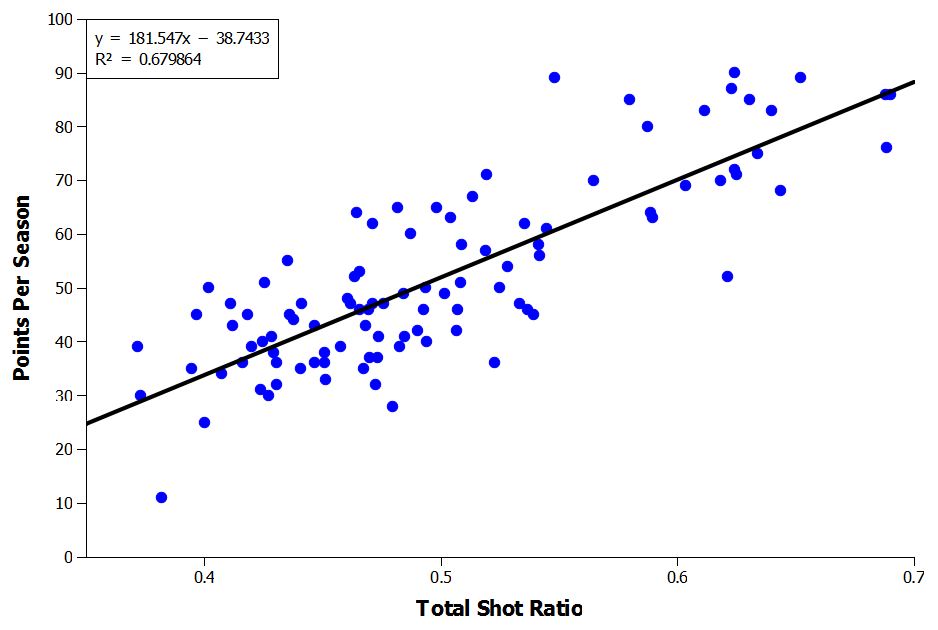Figure 5: Correlation Between Total Shot Ratio and Points
Total Shot Ratio: How Much Data is Enough?
So if Total Shot Ratio is only becoming meaningful over longer periods of time then how much data do we actually need before it becomes a useful metric? To look at this I calculated the overall Total Shot Ratio per season by team and then randomized the order of each match that season. I then looked at how the deviation changed over course of a season compared with the overall ratio, e.g. after five matches, ten matches etc (Figure 6).
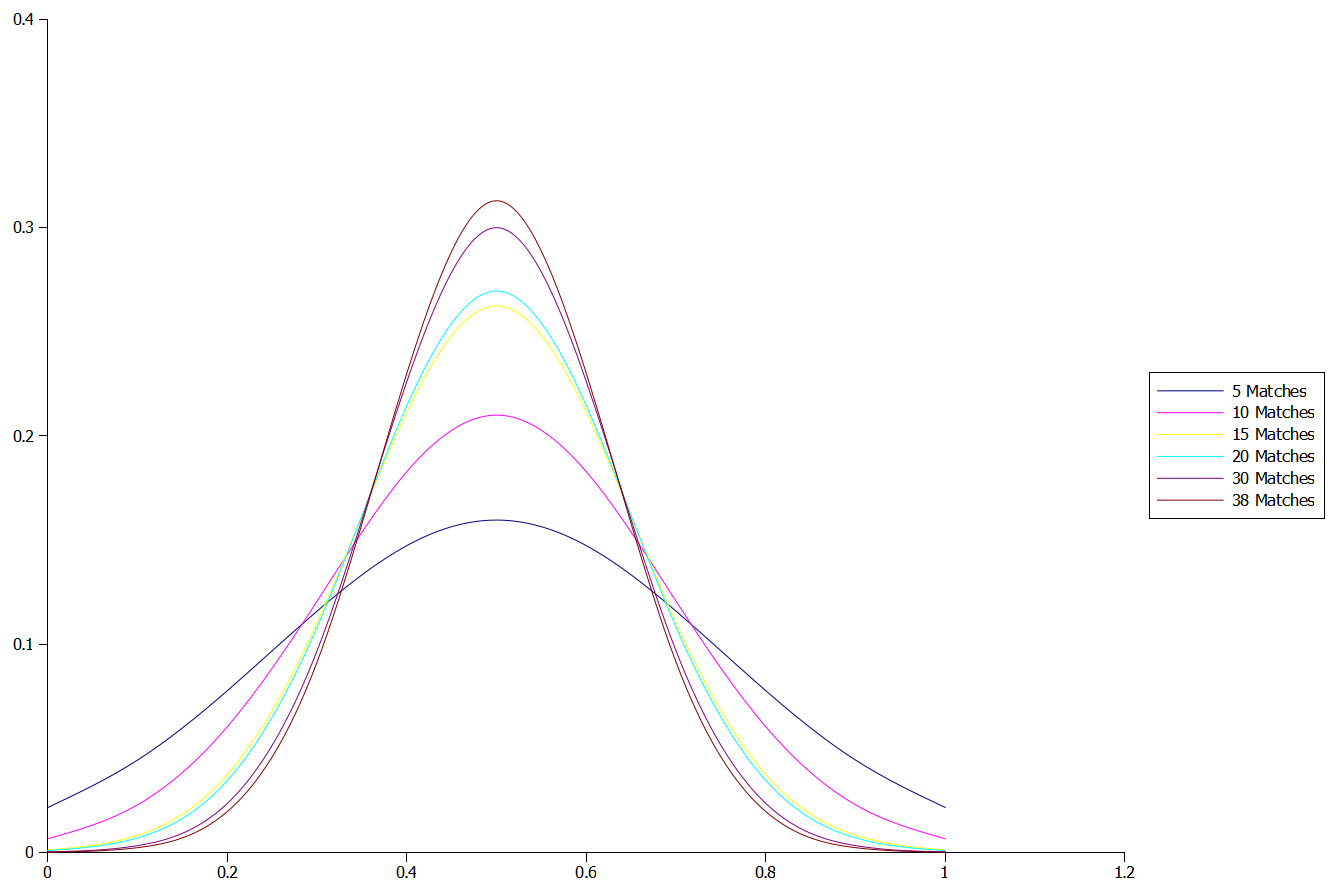Figure 6: Deviation in Total Shot Ratio by Sample Size
As more data is used to calculate the Total Shot Ratio it moves closer towards its true value and the deviation decreases as the effect of any outlier matches becomes less influential. With fewer matches being used to calculate the Total Shot Ratio there is more dispersion and variability in the calculated value. Interestingly, there is still a reduction in the deviation moving from 30 matches to 38 matches, suggesting that we may need at least a full season’s worth of data to get an accurate measure of a team’s Total Shot Ratio.
Total Shot Ratio: Calculated Sample Size
Another option to find out how much data we need is to calculate the sample size required to identify specific differences in Total Shot Ratio. There are a number of different methods for this but the commonly used t-test sample size estimation suggests that to be 95% certain that two teams with a difference in Total Shot Ratio of 0.1 are actually different from each other takes 45 matches.
So, to be statistically certain that a team with a Total Shot Ratio of 0.6 actually has a higher ratio than a team with a Total Shot Ratio of 0.5 rather than it just being down to random variability requires over a season’s worth of matches to be played.
As the differences become smaller then the number of matches required increases even further – to identify a difference in Total Shot Ratio of 0.05 takes nearly five season’s worth of matches!
Conclusions
In the short term, Total Shot Ratio appears to virtually meaningless in terms of goals scored or match outcomes as its variability is so high.
Over the long term though, skill outweighs luck and Total Shot Ratio becomes increasingly correlated with outcomes. However, it may take a long time for this to occur and may be less accurate than other statistics available if you are interested in predicting performance.
Finally, this article is not intended to say “do not to use Total Shot Ratio” as it is still an interesting metric. Rather, make sure that you are aware of its abilities and limitations if you are planning on using it for analysis.
Comments
Bob - April 2, 2013
You’re getting closer to the holy grail. Quality of shot data is important. TSR can be refined into something slightly less random (though shots alone are still less random than goals).
Martin Eastwood - April 2, 2013
I totally agree, the quality of shots are important. You can improve your TSR by taking lots and lots of shots but they are not necessarily going to improve you chances of scoring. It is the quality of shots that are important not the amount of them.
sidereal - April 2, 2013
A good compromise might be looking at shots in the box rather than overall shots. It’s a little bit more recordkeeping (though Opta has them for leagues it tracks) without having to subjectively evaluate shot quality. And I suspect it’d correlate better over a shorter sample size. I can run the correlation between TBSR and results in MLS when I get some time.
Martin Eastwood - April 2, 2013
Sounds good, would be interesting to see how the correlation looks
sidereal - April 4, 2013
Had time to run this today. With two years of MLS data I found substantially lower correlations than your EPL data. Possibly because of the smaller sample size. More likely because MLS shot quality is lower and more random.
R squared for TSR to goals is 0.0245 and to GD is 0.05. Switching to box shots improves those marginally to 0.042 and 0.087.
But at the season level the improvement mostly goes away. TSR to seasonal PPG is 0.324 and TBSR to seasonal PPG is 0.349.
Martin Eastwood - April 4, 2013
Thanks, that is really interesting to see!
There is also much more parity in the MLS compared with other leagues too, which may be having an effect as the more closely matched the teams are then the more impact luck has on determining outcomes.
Bob - April 2, 2013
It isn’t actually that difficult to measure quality of shots, as long as you’re prepared to put in 10-15 minutes work per week (per league). For the top five leagues in Europe anyway, plus a few others (including the npower leagues from next season).
I agree shots alone has it’s limitations but over a 20-25 game sample, I do think TSR is an extremely valuable measure and one that has called a few regressions this season (Sunderland the most obvious) that most observers did not see coming.
shuddertothink - April 3, 2013
What would be the best way to quantify ‘shot quality’?
The best we have on ‘shot quality’ is Shots on target to points has an r2 of .0685 in 2012/13.
There may be issues with the sample size of just 600 data points in comparison to 7600 or so in Martin’s 10 year sample.
As was stated skill outweighs luck given a bigger sample
Turkish - November 29, 2013
Do you teach any courses at the moment on football based prediction?
I am sure a lot of people would be keen to see you present your information – would you be interested on doing that?
Martin Eastwood - December 4, 2013
Hi Matthew,
I don’t have any courses planned but it would be something really interesting to do if there was enough interest from people!
Cheers,
Martin
Dzof - June 14, 2014
Thanks for the article, very interesting.
Do you have the numerical values for figure 4 published anywhere (Correlation between shot ratio and goal difference)? Or raw data?
I basically was looking for the observed probability a team wins/draws/loses a game given a certain shot ratio, e.g. When a team has 60-70% shot ratio, what % of games do they win?
Extending this, the other question that comes to mind is if this probability is consistent across seasons / teams / leagues.
Keep up the good work!
Martin Eastwood - June 14, 2014
Not to hand but I’m planning an update to the site over the summer to provide access to that sort of thing so keep an eye out for that!
Michael - October 31, 2014
Thanks for the article. I was looking for statistics like that! You said there are other statistics for predicting performance which are more accurate than the TSR. Which ones were you talking about?
Martin Eastwood - October 31, 2014
Hi Michael, thanks for the message. Take a look at expected goals to start with :)