Understanding Elo Ratings
What are Elo Ratings?
The Elo rating system was originally devised by its creator Arphad Elo as a way to calculate the average skill levels of two chess players. Although the system was created specifically for chess it has also been adapted to many other games and sports, including international football.
How Do They Work?
The fundamental principle behind Elo ratings is that the performance of a team in each match can be considered a random variable sampled from a normally distributed population centred on the team’s true skill level. Although performances will vary from match-to-match, the true skill level of the team is likely to only change slowly over time so can be considered to be the mean value of all their performance values.
For example, Figure one shows a team with an Elo rating of 1500. On any given day their actual performance could vary from anywhere below 1000 to above 2000. But over a reasonable period of time their performances will average out to 1500.
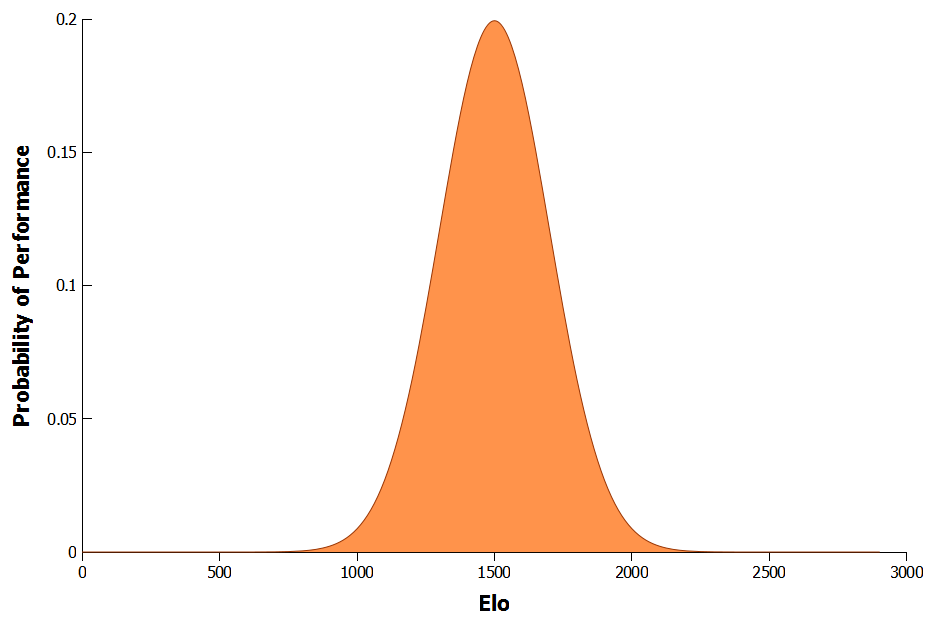
Figure 1: Possible performances for a team with Elo of 1500
Why are Elo Ratings Useful?
Elo ratings have no units and taken in isolation their specific values are of little interest. However, they become useful when comparing teams together as they can be used to determine the expected outcome between two teams based on the difference between their Elo ratings.
The range used for Elo ratings is somewhat arbitrary with Elo himself suggesting they should be scaled so that a difference of two hundred points equates to the higher ranked team having a win probability of 75%. In addition, Elo ratings are generally scaled so that an average team has a rating of 1500.
Predicting Match Results Using Elo
Plotting two team’s Elo distributions together gives a nice way of visualizing their expected performances. Figure 2 shows Team 1 with an Elo rating of 1100 compared with Team 2 with an Elo of 1500. The most likely outcome is that both teams will play to their average ratings and so Team 2 will win overall as they have the higher ranking. However, both team’s performance distributions overlap each other, so it is possible for Team 1 to out perform Team 2 and win the match.
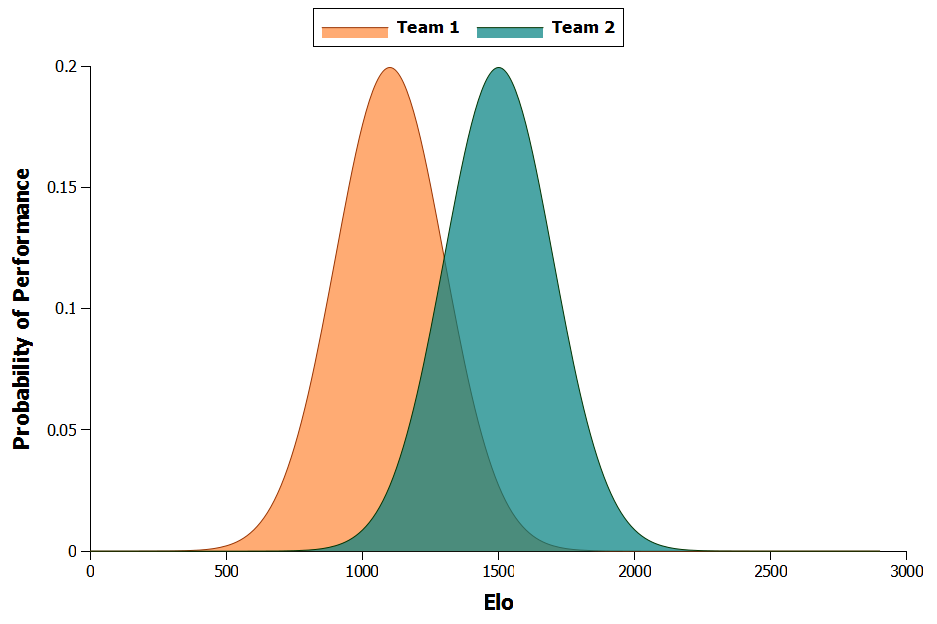
Figure 2: Comparision of two team’s Elo performance probabilities
The more these performance distributions overlap then the greater the chance of the lower placed team winning the match. The actual probability of victory can then be calculated from these two distributions by subtracting one from the other to get the normal difference distribution between the two (Figure 3).
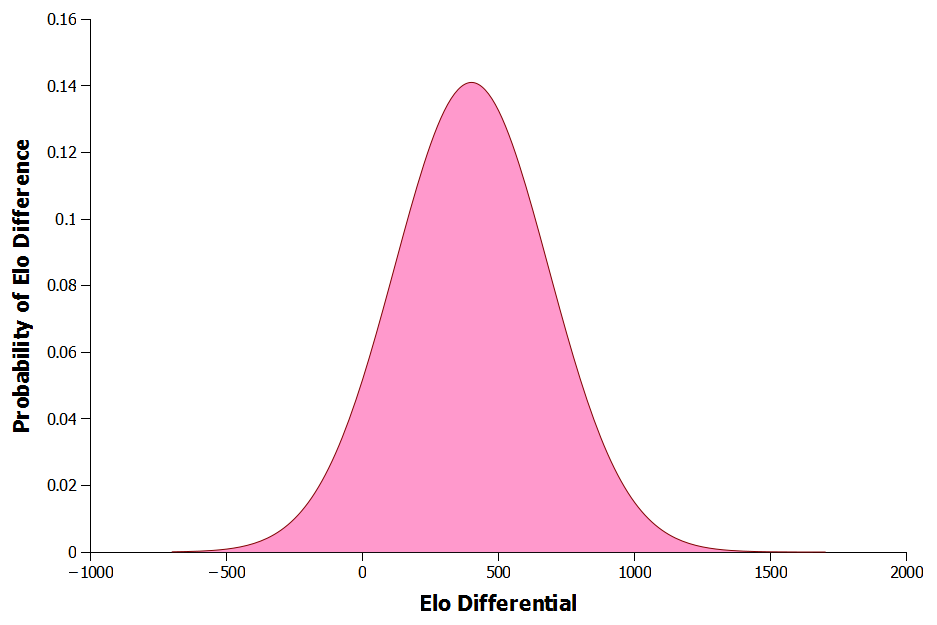
Figure 3: Probability of Elo differential occurring
The centre of this new distribution is equal to the difference between the two ratings (1500 – 1100), meaning the most likely outcome is that Team 2 play like a team with an Elo rating of four hundred higher than Team 1. As we move further to the left the difference between the two teams decreases until we reach a negative differential at which point Team 1 actually start to play better than Team 2, albeit with a low probability of occurrence.
The actual probability of this occurring can be plotted using cumulative frequency to show the overall chance of winning based on the Elo differential (Figure 4). So for our example above, Team 1 with its differential of -400 actually has around a 9% chance of winning the match while Team 2 has a 91% chance of winning.
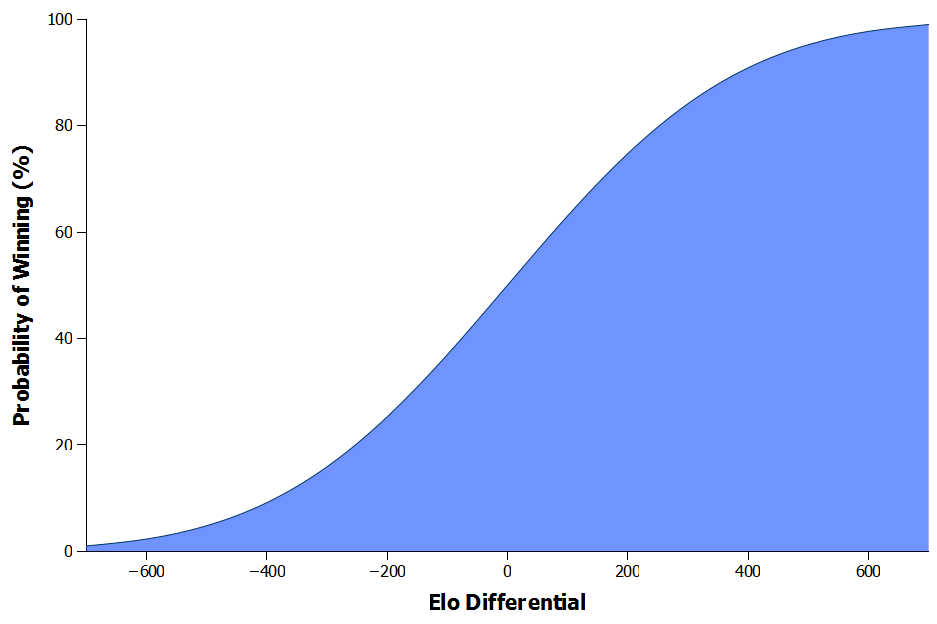
Figure 4: Probability of winning based on Elo differential
So now we understand the theory behind Elo ratings, my next post will look at how they can be calculated and applied to football teams.
Comments
Lars - February 1, 2013
“two hundred points equates to the higher ranked team having a win probability of 75%. Following this advice means that an average team should have an Elo rating of 1500.”
That conclusion is false. The win probability would be exactly the same if the average Elo rating was 2500 or 9500. The Elo scale is not absolute, only the difference between teams’ Elo values is relevant.
Apart from that very good introduction, congratulations. I am really looking forward to the sequel.
Martin Eastwood - February 2, 2013
Good point Lars, I have re-phrased that sentence to avoid any confusion.
Thanks for the feedback!